Building epic, multiplexed, and nano-enabled systems
 We have developed a MEMS packaging technology that relies on mesoscaled DRIE-patterned deflection springs to integrate electrostatic lenses to massive arrays of high-voltage devices with great precision and repeatability.
We have developed a MEMS packaging technology that relies on mesoscaled DRIE-patterned deflection springs to integrate electrostatic lenses to massive arrays of high-voltage devices with great precision and repeatability. Scaling-down and multiplexing chemical reactors (for example, the MEMS singlet oxygen generator shown) increase their efficiency, enabling a wide range of portable applications.
Scaling-down and multiplexing chemical reactors (for example, the MEMS singlet oxygen generator shown) increase their efficiency, enabling a wide range of portable applications.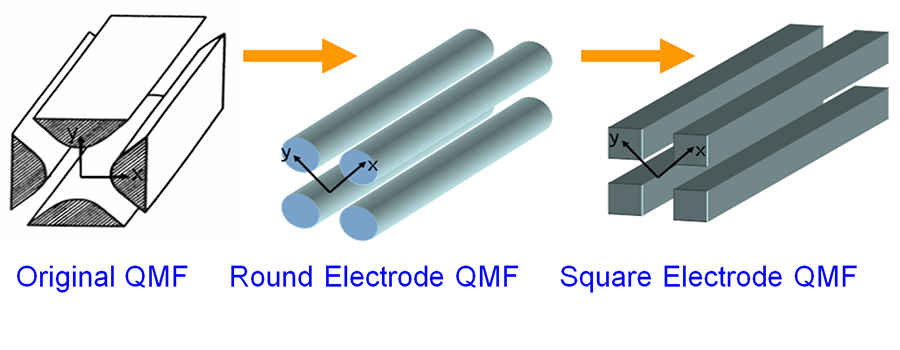 Evolutionary road of miniaturized QMFs to achieve high performance and batch fabrication | Read more…
Evolutionary road of miniaturized QMFs to achieve high performance and batch fabrication | Read more… Massive arrays of individually ballasted field emitters are the key to implement reliable high-current cathodes.
Massive arrays of individually ballasted field emitters are the key to implement reliable high-current cathodes. Carbon nanotubes can be used to produce localized high electrostatic fields with low voltage, opening the doors to many exciting applications such as portable gas ionizers.
Carbon nanotubes can be used to produce localized high electrostatic fields with low voltage, opening the doors to many exciting applications such as portable gas ionizers. Multiplexed electrospray has tremendous potential in a wide range of exciting applications, e.g., manufacturing, analytical instruments, and nanosatellite propulsion.
Multiplexed electrospray has tremendous potential in a wide range of exciting applications, e.g., manufacturing, analytical instruments, and nanosatellite propulsion.
 |
 |
 |
 |
 |
We thank our former and current sponsors for their support:
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
