Paul Penfield,
Jr., Information and Entropy,
BEACS, informal MIT study group, Cambridge, MA; May 16, 2001.
Information and Entropy
Information and Entropy
Outline
| o | Arcane |
| Pity |
| Perspective |
| Information |
| Course |
| Status |
The Second Law of Thermodynamics
Surely one of science's most glorious accomplishments
Also one of the most profound and mysterious
What is this thing called "entropy?"
Does the Second Law really tell us which way clocks run?
Deep related concepts
Complexity
Randomness
Fluctuations
Dissipation
Order
The public's imagination is captured
Nobody really understands it
At least that is what we believed as graduate students
It is too complex to be taught
Why is entropy considered arcane?
Because people think it is part of thermodynamics
Thermodynamics really is hard to understand.
Many concepts -- heat, work, temperature, ...
You have to care about things like ideal gases.
Most engineers don't need to know thermodynamics.
Most don't care.
Information and Entropy
Outline
| Arcane |
| o | Pity |
| Perspective |
| Information |
| Course |
| Status |
This is a shame
Entropy and the Second Law are taught as part of thermodynamics, so most people miss them.
... and thereby miss something pretty important
All scientists, all engineers, indeed all educated people need to understand that some operations are reversible and some are not.
They need to be able to tell them apart.
They need to know there is a way to quantify reversibility.
They need a "monotonic model"
To complement models of conserved quantities
Both are helpful for understanding the world
Both are prototypes for other quantities
Can we satisfy these very real needs somehow?
They have nothing to do with thermodynamics.
But that is where they have traditionally been taught.
Information and Entropy
Outline
| Arcane |
| Pity |
| o | Perspective |
| Information |
| Course |
| Status |
Entropy is useful outside of thermodynamics
Thermodynamics always involves energy
Entropy need not (at least at one level)
Outside of thermodynamics, disregarding energy
Entropy is less complex
There are plenty of reversible and irreversible operations
The Second Law, or something much like it, exists
Monotonic models can be taught more easily
In a more general context, concepts must be simpler
This is the secret of making complexity simple
War is too important to be left to the generals*
And entropy is too important to be left to the physicists
* George Clémenceau (1841 - 1929)
French Premier, 1906 - 1909, 1917 - 1920
Information and Entropy
Outline
| Arcane |
| Pity |
| Perspective |
| o | Information |
| Course |
| Status |
Information theory
Information is abstract, independent of physical form
This is the fundamental mantra of the information age
Information theory quantifies information or uncertainty
How much information, not what it is or what it means
It is information about something, so is relative
It is your uncertainty, or mine, so is subjective
Information theory is arcane
Applications use advanced math, so taught at graduate level
Information cannot exist without a physical form
Historically
Cost of information dominated by cost of artifacts
Moore's law reducing this cost
Where will it all end?
The mantra ultimately fails because of quantum mechanics
In the quantum limit thermodynamics and info theory both fail
Are information and entropy really the same?
Same formula (sum of p log p)
Shannon believed this was not a fundamental identity
As far as I know Jaynes agreed
The question is, can we convert from one to the other?
Vastly different scales
Our approach
They are the same concept
Information is physical
Entropy is subjective
Both are relative
One can be traded for the other (with experimental difficulty)
We should think about entropy conversion systems
The ideas are simple, the applications are arcane
Unifying the concepts simplifies them and lets freshmen in
The basic idea in teaching them together
Start with information
Entropy is one kind of information -- information we don't have
See reversible and irreversible data transformations
In computation and communications
Note that irreversible operations destroy information
They also give meaning to causality and the direction of time
This is the Second Law in this context
Apply to a physical system with energy
Use principle of maximum entropy
Voila, thermodynamics!
Temperature is energy per bit of entropy (sort of)
Second Law in traditional setting
Carnot efficiency
Trade information and entropy in Maxwell's demon
We are teaching this stuff to freshmen
Why is this possible?
Today's students are different
Best to start from the known
Data, disks, Internet, packets, bits, ...
Consistent with the coming information age
Go toward the unknown
Thermodynamics, equilibrium, heat engines, refrigerators
Relevant to the current industrial age
Physical view of information . . . like energy, information
can be of many types
can be converted from one form to another
can exist in one place or another
can be sent from here to there
can be stored for later use
There are interesting applications
Biology (e.g., genetic code)
Communications
Quantum information
Information and Entropy
Outline
| Arcane |
| Pity |
| Perspective |
| Information |
| o | Course |
| Status |
A Freshman Course
Spring semester, 6 units (half a normal MIT course)
12 weeks (Spring 2001 outline):
1. Bits and Codes (perhaps next year qubits)
2. Compression
3. Errors
4. Probability
5. Communications
6. Processes
7. Inference
8. Entropy
9. Physical Systems
10. Energy
10. Temperature
12. Quantum Information
This course is NOT
Introduction to Computing
Introductory Communications
Thermodynamics 101
Course material
1. Bits
Restoring logic
Digital abstraction
Signals and streams
Boolean algebra
Codes
Bytes
Symbols
Fixed-length codes
ASCII
Genetic code
Binary code, gray code
Variable-length codes
Morse code
Telegraph codebooks
Course material (cont)
2. Compression
Helps with low channel capacity
Codebooks
Irreversible -- fidelity requirement
JPEG
MP3
Reversible
Run length encoding
LZW, GIF
The LZW patent issue
3. Errors
Physical sources of noise
Detection
Parity
Correction
Triple redundancy
Hamming codes
Course material (cont)
4. Probability
Racing odds
Random sources
coins, dice, cards
Probabilities are relative and subjective
Information can be quantified
5. Communications
Model with source, coder, channel, decoder, receiver
Source coding theorem
Huffman codes
Channel capacity
Lossless
Noisy
Client-server model
TCP and IP
Strategies for recovery from lost packets
Course material (cont)
6. Processes
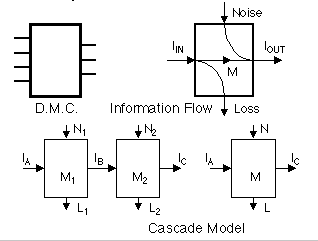
Discrete memoryless channel
Noise, loss
M = IIN - L
= IOUT - N
Cascade inequalities in L, N, and M
L1 <= L
L1 + L2 - N1 <= L <= L1 + L2
7. Inference
Given received signal, what is input
How much information have we learned?
Course material (cont)
Discrete Memoryless Channel
Course material (cont)
8. Entropy
Entropy is information we do not have
It is relative and subjective
Input probabilities consistent with constraints
Minimum bias means maximum entropy
Lagrange multipliers
Simple examples with analytic solution
Examples with one constraint, many states
9. Physical Systems
Quantum mechanics
Multi-state model
Microscopic vs. macroscopic
Course material (cont)
10. Energy
Energy per state
Expected value of energy
Boltzmann distribution
Equilibrium
11. Temperature
One of the Lagrange multipliers is temperature
Heat, work
Carnot efficiency
12. Quantum Information
Qubit
Quantum computation
Maxwell's demon
Pervasive themes
Entropy and Information are the same concept
You can trade one for the other
Difference in scales is being erased by Moore's law
Irreversibility shows up everywhere for the same reason
Examples from many areas, including biology
Discrete memoryless channel model
Two kinds of physical quantities -- conserved and monotonic
Some of the subtle points
Information is physical and entropy is subjective
What does that say about physics?
Math generally simple -- discrete, not continuous processes
But Lagrange multipliers are not easy
Skill in modeling is still important
No magic here
At the freshman level you cannot go very deeply
All we can do is provide simple ideas to be built on later
We want to be consistent with later learning in specific areas
Basic level teaching requires deeper understanding
It's disturbing to have unanswered questions close at hand
Information and Entropy
Outline
| Arcane |
| Pity |
| Perspective |
| Information |
| Course |
| o | Status |
Can freshmen actually learn this stuff?
We are finding out
Fall 1999, course development
Faculty: Paul Penfield, Seth Lloyd, Sherra Kerns
Spring 2000, pilot offering
Limited to 50 freshmen
Of course we have a Web site -- everybody does
https://mtlsites.mit.edu/Courses/6.095
Spring 2001, second pilot offering
If we are successful (so far so good)
The course will be permanent starting in Spring 2002
We will help other universities start similar courses
We will advocate it as a science exposure in the liberal arts
URL of this page:
https://mtlsites.mit.edu/users/penfield/pubs/beacs-01.html
Created: May 13, 2001 |
Modified: May 23, 2001
Related page: Penfield publication list
Site map |
To Paul Penfield's home page |
Your comments are welcome.
Click here for information on MIT Accessibility